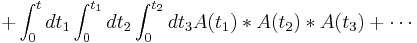Ordered exponential
The ordered exponential (also called the path-ordered exponential) is a mathematical object, defined in non-commutative algebras, which is equivalent to the exponential function of the integral in the commutative algebras. Therefore it is a function, defined by means of a function from real numbers to a real or complex associative algebra. In practice the values lie in matrix and operator algebras.
For the element A(t) from the algebra 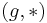 (set g with the non-commutative product *), where t is the "time parameter", the ordered exponential
(set g with the non-commutative product *), where t is the "time parameter", the ordered exponential :\equiv \left(e^{\int_0^t dt' A(t')}\right)_%2B](/2012-wikipedia_en_all_nopic_01_2012/I/43ec8364cd7f71dafb97d5f6feb6febe.png) of A can be defined via one of several equivalent approaches:
of A can be defined via one of several equivalent approaches:
- As the limit of the ordered product of the infinitesimal exponentials:
where the time moments 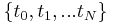 are defined as
are defined as 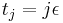 for
for 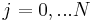 , and
, and 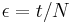 .
.
- Via the initial value problem, where the OE[A](t) is the unique solution of the system of equations:
- Via an integral equation:
- Via Taylor series expansion:
See also
- Related: Path-ordering describes essentially the same concept.
 =
\lim_{N \rightarrow \infty} \left\{
e^{\epsilon A(t_N)}*e^{\epsilon A(t_{N-1})}* \cdots
*e^{\epsilon A(t_1)}*e^{\epsilon A(t_0)}\right\}](/2012-wikipedia_en_all_nopic_01_2012/I/60c9012e556a43241f961c4a854dcaf5.png)
}{\partial t} = A(t) * OE[A](t),](/2012-wikipedia_en_all_nopic_01_2012/I/fed7cabf158bb080eac7e1894dce3514.png)
 = 1.](/2012-wikipedia_en_all_nopic_01_2012/I/bb705fd0ddb6c34ac57d7f305eec737b.png)
 = 1 %2B \int_0^t dt' A(t') * OE[A](t').](/2012-wikipedia_en_all_nopic_01_2012/I/4e10d113b3711dba04e7a3060131d151.png)
 = 1 %2B \int_0^t dt_1 A(t_1)
%2B \int_0^t dt_1 \int_0^{t_1} dt_2 A(t_1)*A(t_2)](/2012-wikipedia_en_all_nopic_01_2012/I/3b7296f92393a8ea0a1069872aecf8c3.png)